No one uses it rightly, as a thing that in every way is apt to draw men toward being.
Plato, Republic, Book VII, 523a
Nobody teaches arithmetic anymore, not in the way the ancients understood it. Walk into any elementary mathematics classroom today, and you'll find students drilling multiplication tables, calculating percentages, and solving word problems. What you will rarely find is the contemplative study of number itself: the profound patterns that emerge when we examine odd and even numbers, the mysterious properties of primes, or the elegant relationships between deficient, perfect, and abundant numbers. We have reduced the mathematical arts to mere computation, trading the wonder of arithmetikos for the utility of logistikos.
Mathematics as a Liberal Art
This reduction of mathematics to mere utility represents a fundamental departure from the classical understanding of mathematical education. In his Introduction to Arithmetic, Nicomachus of Geresa, writing in the second century AD and deeply influenced by Pythagorean traditions, distinguishes between the four sciences of mathematics that we now call the “quadrivium” of the seven liberal arts. For Nicomachus, these mathematical disciplines were not merely practical tools but pathways to philosophy:
“...without the aid of these, then, it is not possible to deal accurately with the forms of being nor to discover the truth in things, knowledge of which is wisdom, and evidently not even to philosophise properly…”
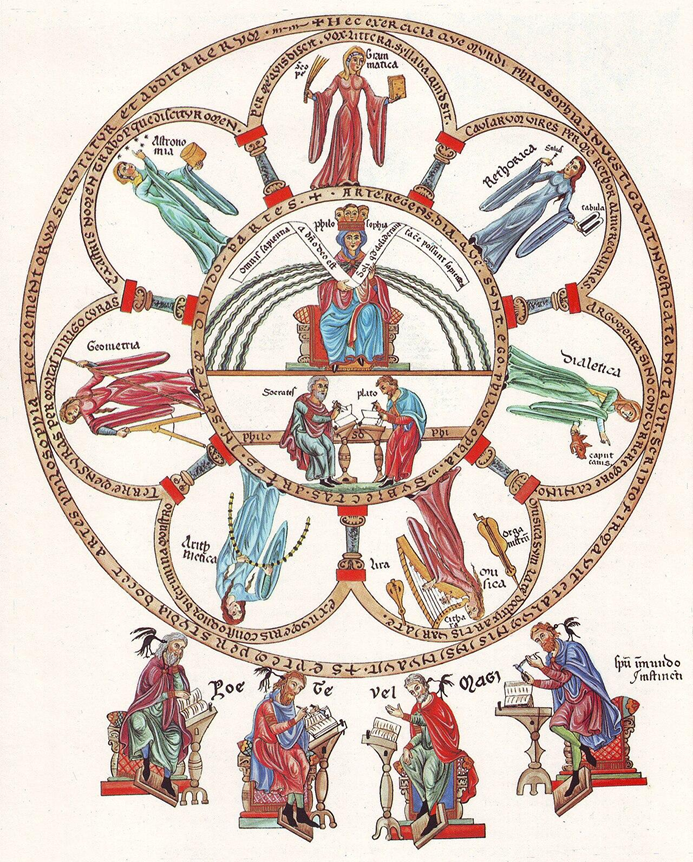
The seven liberal arts surround philosophy at the center.The Hortus deliciarum (“Garden of delights”) by Herrad of Landsberg (source).
The quadrivium of arithmetic, geometry, music, and astronomy composes the greater half of the seven liberal arts. Yet so often they are sidelined in schools claiming to use a truly liberal arts curriculum. The false dichotomy between STEM schools and liberal arts schools is testimony to this. In STEM schools (and most schools for that matter) mathematics receives abundant class time and resources but with a focus on its usefulness. Perhaps as a quiet rebellion against STEM’s overemphasis on utilitarian mathematics, classical and liberal arts schools tend to swing to the opposite extreme. Ironically, these schools tend to teach utilitarian mathematics, and they tend to relegate mathematics to playing second fiddle to the "real" liberal arts of the trivium (grammar, rhetoric, and logic) and the humanities. Ironically, such liberal arts schools tend to teach utilitarian mathematics just as STEM schools do. In both cases, students are denied access to authentic mathematics.
The question of how to teach mathematics at a liberal arts school remains crucial for anyone serious about educational reform. If we genuinely seek to revive liberal arts education and honor the classical tradition rather than merely adopting its vocabulary while perpetuating modern fragmentation, then the quadrivium must be not only remembered but fully restored to its rightful place. This restoration requires more than adding "Liberal Arts Mathematics" courses to the curriculum or including Socratic dialogue with great books. It demands a fundamental reconceptualisation of what mathematics education should accomplish and how it should proceed.
Logistics vs. Arithmetic Distinction
And all arithmetic and calculation have to do with number? Yes.
And they appear to lead the mind towards truth? Yes, in a very remarkable manner.
Republic, Book VII, 525a-b
Book VII of Plato's Republic includes the renowned cave allegory, perhaps the most famous metaphor in all of Western philosophy. What few people ever discuss, however, is Socrates' continued conversation with Glaucon immediately following the allegory. Having described the prisoner's journey from darkness to light, Socrates turns to the practical question: what specific disciplines are best suited to aid the soul in its ascent from shadow to reality? After careful deliberation, they settle on the quadrivium: arithmetic, geometry, astronomy, and music. This consensus is remarkable coming from Socrates, a philosopher famous for professing ignorance and questioning all received wisdom. It would seem that there was one thing Socrates knew for certain: these four mathematical arts possess a unique power to draw the soul toward being itself.
Plato draws a crucial distinction between the art of calculation and the theory of number (Republic, 523a-525a). While calculation serves as necessary preparation, it is only the theory of number that possesses the power to draw the human soul toward being itself. This distinction becomes crystal clear when Glaucon praises the calculation for its usefulness in warfare and commerce. Socrates responds with characteristic irony:
“‘You amuse me,' said I, 'because you are like one who fears the crowd lest you seem to enjoin useless studies. It is, however, not at all a trifling matter, but a difficult one to believe that in these studies some instrument of every man's soul is cleansed and rekindled, which was being destroyed and blinded by his other pursuits, a thing more worthy to save than countless eyes : for by it alone is truth beheld.'"
This pointed reaction reveals Socrates' educational philosophy in its starkest form: the studies he champions are emphatically “useless”. Their value lies not in practical application but in their unique capacity to purify and illuminate the intellect, the eye of the soul.
This Platonic distinction between calculation and theory of number has been recognised by modern historians of mathematics. Sir Thomas Heath, the great translator of Euclid and chronicler of Greek mathematics, and David Eugene Smith, the pioneering American historian of mathematics, both make reference to this fundamental division in ancient mathematical education. The Greeks encoded this distinction in their very vocabulary: logistikos (λογιστικος) refers to the art of calculation or "reckoning," the manipulation of numbers for practical ends, whereas arithmetikos (ἀριθμητικος) denotes the science of number itself, the contemplative study of numerical relationships and properties.
The purpose of learning logistikos is transparently utilitarian: to manage business transactions, solve engineering problems, and navigate the quantitative demands of daily life. The purpose of learning arithmetikos is entirely different and infinitely more profound: to draw the soul toward being itself and prepare the mind for the contemplation of eternal truth.
Elementary Arithmetic is Really Logistike
The ultimate standard of relevance for any topic in mathematics class today is straightforward utility: will this help students balance checkbooks, calculate tips, or pursue STEM careers? Beauty and truth, the very qualities that once made mathematics a pathway to wisdom, tend to be dismissed as luxury items, pleasant but ultimately dispensable. Instead, children are promised merely temporal goods as the reward for their years of mathematical labor: better test scores, college admissions advantages, and future earning potential. This utilitarian philosophy permeates every level of curriculum design. Textbook publishers organise content around "real-world applications". State standards emphasise measurable skills over mathematical insight. Administrators justify mathematical requirements by pointing to economic competitiveness rather than intellectual formation.
Consider what happens when an educator attempts to justify mathematical content on the basis of its intrinsic beauty, profound truth, or sheer intellectual fascination. At a classical or liberal arts school, such arguments will typically be praised and encouraged, but only as enrichment, only after you've covered "everything else that you need to get through". The content that is less beautiful, less intellectually stimulating, but demonstrably more useful for practical purposes (logistikos) remains the curricular foundation. Meanwhile, the more profound arithmetikos content gets relegated to supplemental status, squeezed in when time and attention permit.
This is entirely backward. What we treat as supplemental, the ancients considered foundational. What we prioritise as essential, they viewed as merely preparatory.
According to the classical understanding, logistikos serves as preparation for arithmetikos, the study of real mathematics. The proper educational sequence should involve mastering the basic computational skills of logistikos efficiently, then ascending to explore the beautiful and profound world of arithmetikos, where students encounter the eternal patterns and relationships that constitute deeper mathematical truths. Instead, our current system traps students in what the ancients would have recognised as a servile art, not a liberal art. Year after year, they practice calculation and manipulation, catching only occasional glimpses of genuine mathematical beauty, like prisoners who see shadows dancing on the cave wall but never turn toward the light at the opening.
Only in precious few corners of the modern curriculum do students encounter the nature of numbers themselves: the fundamental distinction between odds and evens, the mysterious distribution of primes and composites, the elegant symmetries of negatives and positives. Every school teaches about square numbers at some point, but in what school do students explore the full family of polygonal numbers that includes triangular, pentagonal, hexagonal, and beyond? Classical schools pride themselves on teaching the cardinal and theological virtues, but do their students learn about deficient, perfect, and abundant numbers, mathematical concepts that once carried profound moral and metaphysical significance? These numerical relationships, which fascinated Pythagoras, Nicomachus, and countless other mathematical philosophers, have been relegated to the margins of education or abandoned entirely.
Way Forward: Teach Real Arithmetike
If, as Socrates, Nicomachus, and Boethius all insist, the study of the quadrivium provides essential preparation for thinking clearly about fundamental questions, then perhaps we need look no further for an explanation of our culture's intellectual confusion. We don't really study mathematics rightly, and the consequences extend far beyond the mathematics classroom itself.
Fortunately, we have models for authentic mathematical education. True arithmetic (arithmetikos) is presented to us in the works of master-teachers like Nicomachus of Gerasa (Introduction to Arithmetic) and Euclid (The Elements, Books II, V, VII, VIII, IX, X). These ancient texts reveal mathematics as a pathway to wisdom rather than merely a collection of computational techniques. However, these works are too sophisticated for elementary students to read directly. This creates a pedagogical challenge: how do we make the profound insights of classical arithmetic accessible to young minds? What is the way forward?
Recent scholarship offers some guidance for this pedagogical challenge. An article from the Notre Dame Medieval Institute distinguishes between three different approaches to quadrivium education: the Boethian sequence (beginning with arithmetic), the Calcidean sequence (beginning with geometry), and the Capellan sequence (beginning with music). This research encourages educators to make informed decisions about which mathematical art should provide the foundation for the others.
Some might object that arithmetic in its true, contemplative sense is only accessible at the college level through advanced courses like number theory. This argument, however, rests on a misunderstanding of arithmetikos. Arithmetikos is not identical to modern number theory. Modern mathematical machinery (algebra, calculus, etc.) is necessary for the study of modern number theory, but is not required for the study of arithmetikos. The ancient Greeks achieved profound insights into the nature of number without algebra, without calculus, and even without the decimal positional notation system we take for granted. Their methods were often more elementary yet philosophically richer than our own.
The way forward requires nothing less than a complete re-evaluation of the elementary mathematics curriculum. The current curriculum organises instruction around computational skills and practical applications. These skills of logistikos need to be relegated to their proper place as means to the higher end of arithmetikos. First, we must identify the skills proper to logistikos that are essential to preparation for arithmetikos. Second, concepts and ideas from Nicomachus, Euclid, and other masters of arithmetikos must be repackaged as grade-level, essential content, not supplemental material.
This is a hard task. The modern curriculum, with its focus on the practical, useful components of logistikos, is ideal for a standards-based, measurable approach. The skills of calculation and computation are essentials to be mastered, but not as ends in themselves nor for their usefulness. These skills and means to the end of beholding and contemplating beautiful truths of arithmetikos, the theory of number. To that end, perhaps an ideal curriculum would be punctuated with end-of-chapter arithmetikos work on primes, perfect numbers, polygonal numbers, or Egyptian fractions. These textbooks do not yet exist, however, so for the time being excellent teachers enmesh these arithmetikos lessons into the modern curriculum.
Were an integrated curriculum of this kind developed, it would progress systematically from concrete to abstract, from simple to complex, building students' capacity for mathematical contemplation year by year. The ultimate goal would be to prepare students for direct engagement with the great mathematical texts themselves: the works of Nicomachus, Euclid, Apollonius, Archimedes, and their successors. Rather than encountering these masterpieces as foreign and intimidating documents, students would approach them as familiar territory, having spent years developing the intellectual habits and foundational knowledge necessary for genuine understanding.
The Suit Must Fit
There is no ideal curriculum that fits every school. A good curriculum can only be determined in light of a school's fundamental mission and educational philosophy.
Some institutions may legitimately choose to provide primarily technical training, preparing students for immediate entry into the workforce as engineers, architects, accountants, and scientists. Such vocational preparation serves an important social function and meets genuine economic needs. There is nothing inherently wrong with schools that prioritise logistikos (practical mathematical skills required for professional competence) provided they are honest about their goals and methods. In the words of David Eugene Smith:
“There is, however, one principle that should guide us in the consideration of this phase of the question: Whatever pretends to be practical in arithmetic should really be so.”
Other schools, however, might seek the (arguably) higher goal of preparing children for the intellectual life, for the study of philosophy, the pursuit of wisdom, and the contemplation of the true, the good, and the beautiful. Schools committed to this classical vision cannot content themselves with teaching mathematics as mere computation. If they truly seek to form students capable of philosophical inquiry, they must recover the ancient understanding of arithmetikos as a pathway to truth. Only then will mathematics resume its rightful place among the liberal arts, serving not as a practical tool but as a means of intellectual and spiritual formation.






